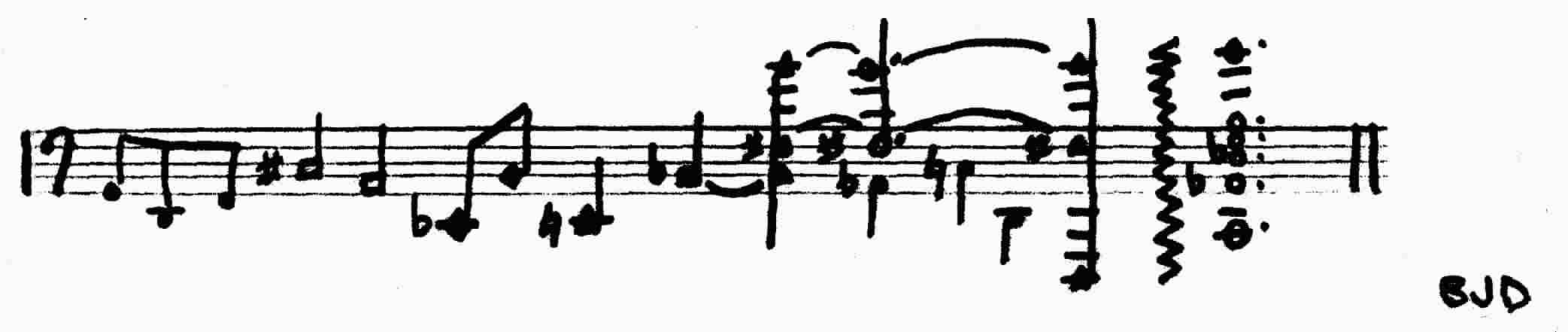Fractional Meter Primer
by Barry Drogin
Back to guide - Next item in guide - Back to index - Next item in index
The king went to his blacksmith with a request for a golden platform. The dimensions
were to be simple. It was to be a perfect square one foot high, and made of solid gold. The king
wanted it as big as possible so he gave the blacksmith a large amount of gold --- 10 cubic feet.
The king could afford no more. The king also made it clear to the blacksmith that every bit of
gold was to be used, and that there were to be no impurities, or the king would have the
blacksmith's head.
Anxious for such a large commission, the blacksmith agreed to the job, but soon started to
worry. His tools were only so accurate --- how could he divide 10 square feet into two parts (i.e.
square root of ten)? Perhaps he could return a cubic foot?
"No!" yelled the king. "You fool, anyone can make a square out of four equal sides!
What could be simpler? Very well, then, make it circular instead."
I made up this story to demonstrate how ideas that anyone can understand can become
quite complex in application. The concepts of time and rhythm I will attempt to explain will
hopefully sound very simple and perhaps obvious to the layman. The application of these
concepts, though, has required the construction of a music machine, the Rhythm Combiner, and
the resurrection of a little known notation system, invented by Henry Cowell, for its realization.
The present notation system was invented for ease --- the blacksmith demands that all volumes
given him be perfect squares. Perhaps the blacksmith will now hire an engineer to help him
mathematically or mechanically approximate the length he needs to an accuracy previously beyond
the capabilities of his crude tools and untrained eye.
Enough of this analogy, let us move to a more direct one. Let's create, in our mind, a
constant beat, or pulse. I strongly recommend that the reader stop at this point and actually
imagine a good number of beats rather than take my conclusions on faith. Stop reading.
Okay, what happened? Even though we were imagining it, and it was a mental process,
perhaps the body attempted to get into the act. Maybe you started to swing back and forth. Or
your foot moved up and down. Perhaps it felt like something was passing by, like a rope, with
knots tied at equal intervals. In all cases, we are wrapped up in motion, and a constantly
repeating motion at that. Is this motion back and forth, like the swinging, or merely the same
element being repeated, like the foot tap, or shall we let into our feeling a sense of getting
somewhere, a feeling of triumph when each knot successfully appears when it should? Since we
will be talking about music, it is obvious that for our purposes the last analogy fits best, since it
allows for a creative process. We could adjust the other two analogies to fit our needs: perhaps
the swing body wishes to move also along curves in space, as in a waltz---the partners swing left
and right, but also can move in creative patterns around the floor. Perhaps our foot tapping can
be thought of as walking---in that case we would have a destination in mind and could watch the
scenery as we go.
But let's get back to our rope. As a composer, I tend to feel that the rope comes from
some invisible orifice on my body and travels out to other people. Perhaps you see the rope
coming towards you, or passing from left to right. It doesn't matter as long as we both can see
the straightness of the rope and the regularity of the intervals marked on it.
While watching the rope, let's listen to it.
Do you sometimes wish to stress certain beats? This is natural. Perhaps you started to
count the beats and decided to restart after certain numbers like three, four or eight. Perhaps you
found yourself accidentally stressing every second or fourth note. Psychologists say we naturally
perceive information in groups of two of three.
If we stress the right beats, then, we should be able to produce every rhythm and
syncopation (which is rhythm involving so-called "off-beats" for avoiding continuous groups of
two and using 3+3+2=8 instead, say) known to mankind, right? Well, not exactly. If you
remember, the engineers ran into a problem with the constant beat --- they'd need 5280 of them
every second so they could choose exactly which beat to stress. Obviously there is something else
going on.
This something else is very easily explained when we consider our knotted rope. Suppose
we were to speed up the frequency of the beats. There are two ways to do this---we could move
the rope faster or we could place the knots closer together. Actually, both of these are quite
different but both have their analogies in music.
If we were to move the rope faster, we would probably have to accelerate the speed rather
than merely jump to the higher speed. In music, the term accelerando is used to indicate
acceleration of the tempo. The tempo is the rate of speed of the occurrence of the reference
pulse.
Music would sound rather strange if the only way we could produce rhythms were
through accelerandi and ritardandos (decelerations). If we add on our theory of stressed and
unstressed beats we have moved a step closer to music. By allowing some of the unstressed beats
to not sound at all we have made a quantum leap.
What does that mean in our analogy? If we remove every other knot from our rope, we
find that our speed has been halved. Also, the time between beats has been doubled. At this
point, it will be easier if we learn a little musical notation. In three paragraphs I will teach you the
basics of rhythmical notation! If you are a beginner, take it slow---but I can assure you now that
you will find it very simple.
Our original constant beat is usually represented as a quarter note, which is merely a
black-filled circle with a stem going up or down:  or
or  . The slower note that lasts twice as long
is twice a quarter or a half note, which is drawn the same way as a quarter except the circle is not
filled:
. The slower note that lasts twice as long
is twice a quarter or a half note, which is drawn the same way as a quarter except the circle is not
filled:  or
or 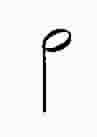 . Twice a half note is a whole note, and we drop the stem:
. Twice a half note is a whole note, and we drop the stem:  . Curiously enough, the
longer the time duration, the less there is to draw. If we were reading and singing or playing a
line of music, we would stare at the bare whole note for a long time, while we would have to
translate the filled, stemmed quarter note much faster!
. Curiously enough, the
longer the time duration, the less there is to draw. If we were reading and singing or playing a
line of music, we would stare at the bare whole note for a long time, while we would have to
translate the filled, stemmed quarter note much faster!
If, instead of eliminating knots from our rope, we added knots, we would double the
speed, or halve the duration. Half of a quarter note is an eighth note, and we add a flag to the
stem:  or
or  . Sometimes when two or more eighth notes are next to each other we connect the
flags, e.g.
. Sometimes when two or more eighth notes are next to each other we connect the
flags, e.g.  becomes
becomes  .
.
Notice what is added at each step:  ,
,  ,
,  ,
,  ,
,  , etc. There is one other symbol we should
know. This does not follow our added-symbol-is shorter-duration rule. If a dot is placed after a
note, the duration is increased by half, e.g.
, etc. There is one other symbol we should
know. This does not follow our added-symbol-is shorter-duration rule. If a dot is placed after a
note, the duration is increased by half, e.g.  , a dotted quarter note, is a quarter plus eighth, or
three eighths,
, a dotted quarter note, is a quarter plus eighth, or
three eighths,  +
+  +
+  .
.
We will not consider rests, which are pauses. We shall consider rests to be simply ways of
telling the performer that he need not hold a note for a long time---after he starts it he can rest
until the next note is supposed to start.
Now we can have a lot of fun with rhythm, as long as we keep using multiples of two.
The length of any space between knots on our rope, when multiplied by some power of two, will
give us the length of the space between quarter note knots, our original constant beat:
 =2-1 x
=2-1 x  ,
,  =21 x
=21 x  ,
,  =3 x 2-1 x
=3 x 2-1 x  .
.
In addition, we can use accelerando and ritardando.
Is that all there is? Say the words, "Multiples of two," aloud twice. Come on, say it! If
we translated this into rhythmical notation, we would get:

What if my grammar was wrong, and I asked you to say, "Multiples by two" instead.
Wondering what I meant, you would probably stress the word "by," and say
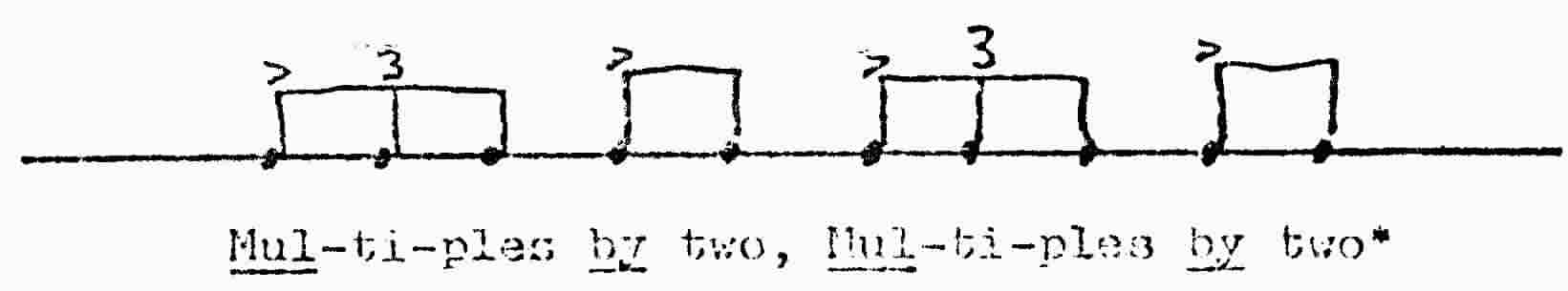
If you clapped your hands on the accents (Mul and by), you would find that their pulse is
constant. It was all right to have two eighths fitting into that quarter note pulse, but what are
those three eighths with a three written on top? This is called a triplet, and it certainly isn't a
multiple of two. In a triplet, a quarter note (or half, eighth, etc.) space is split into three equal
spaces.
Suppose you were one of those people who pronounces the word "multiple" by holding
the syllable "mul" for a little while, in other words:

Notice that there are now three accents to a phrase instead of the two in the other two
cases. This is called compound time and is used for waltzes.
A very strange thing happens when you substitute in the word "by" for "of" as in the
second example. We will have to approach the answer by changing the phrase to "Multiples by
two and":
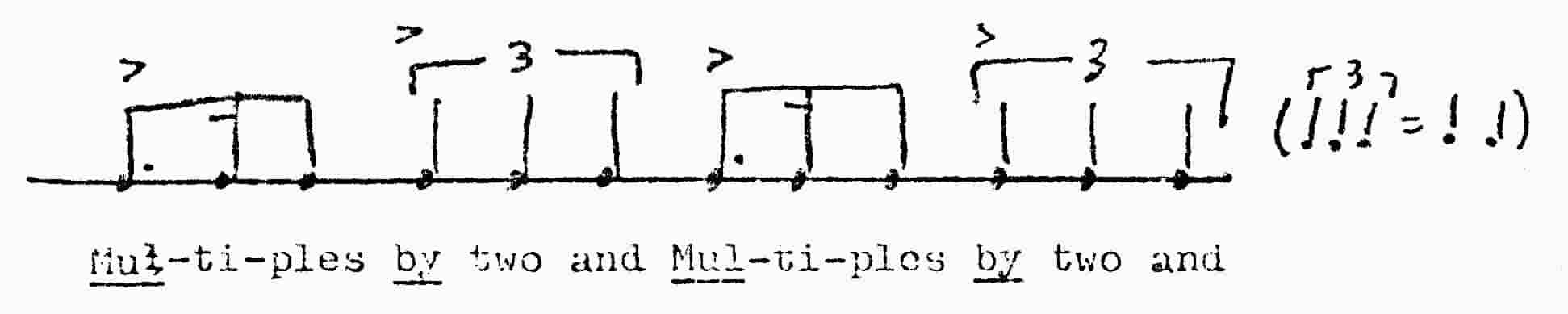
This triplet is slower so we use quarter notes and brackets instead of flags. Since
 =
=  , just as
, just as 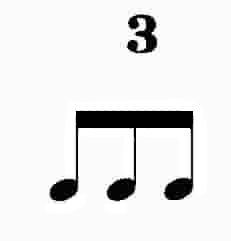 =
=  , if we add up the number of eighth notes we get seven
per phrase. This is not that unusual---many Russian and Hungarian folk songs use this meter
(Meter is the number of units, usually quarter notes or eighths, per phrase or measure. Our
example would be written as 7/8, i.e. seven eighth note durations to a measure). What will shock
most musicians is what happens when we drop the word "and" from the phrase. It is, in fact,
unwritable. Let us look at the rope to see if we have done anything unthinkable.
, if we add up the number of eighth notes we get seven
per phrase. This is not that unusual---many Russian and Hungarian folk songs use this meter
(Meter is the number of units, usually quarter notes or eighths, per phrase or measure. Our
example would be written as 7/8, i.e. seven eighth note durations to a measure). What will shock
most musicians is what happens when we drop the word "and" from the phrase. It is, in fact,
unwritable. Let us look at the rope to see if we have done anything unthinkable.
The first note, on the syllable "mul," is a dotted eighth,  , which equals 3 x 2-2 x
, which equals 3 x 2-2 x  , or three
quarters of the length of a quarter note. The second note, a sixteenth, is the fourth quarter of that
quarter note. The third note is an eighth.
, or three
quarters of the length of a quarter note. The second note, a sixteenth, is the fourth quarter of that
quarter note. The third note is an eighth.  +
+ +
+ =
= =
=


The next three notes were triplets made by splitting a half note ( =
=  ) into three equal
parts. If we were to tie to our quarter note rope, we would do the following:
) into three equal
parts. If we were to tie to our quarter note rope, we would do the following:

1) remove a quarter note:

2) replace with two notes placed at regular intervals:

Musicians will do this without a wince. But if we use only two triplets, we're in trouble,
according to musicians. We're in trouble because there's no way to have a measure of 2/3 --- only x/2n is acceptable.

You may have noticed the slight damage done to the rope. To the right, the other quarter
notes no longer line up! Since we have removed a 2/3  section (
section ( =
= ,
, 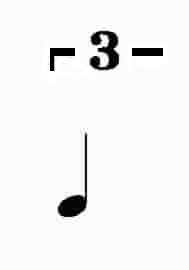 =2/3
=2/3 ), the beat will
now fall always on the .33333... mark. Have we grown too complicated? Why did we use
), the beat will
now fall always on the .33333... mark. Have we grown too complicated? Why did we use  =
= in the first place?
in the first place?
The answer is very simple, but I'd like to show you some old music first. You may be
thinking that these rhythmically complex ideas are merely the musings of someone attempting to
do something "new" for its own sake.
I demonstrated that these rhythms were already present in spoken language. You may
argue that since this is so the rhythms are not music. I do not wish to try to define music for you
so that the word "music" clearly includes the "music" of spoken language. It is a lot easier to
merely show you accepted examples of music that include the rhythms we are talking about.
I cannot show you an example of "discant," because its very nature defies transcription.
"Discant" (and "plainsong") is actually music sung with the rhythms of language --- free and
flowing. It was popular during the Middle Ages.
What's that? Yes, before music was rhythmically notated it was sung in a manner that is
now unnotatable.
I can't show you this music in the present notation system (though we did attempt it in our
"multiples of two" game), but I can show you the next step in the development of musical
notation --- the devising of "mensural" (or measured) music. Mensural music is perfect for our
consideration because it is an attempt to notate discant. Also, scholarly attempts have been made
to translate "musica mensurata" into notation meaningful to the world today. All of these
attempts are written up in German, but we can "look at the pictures" and tell what is going on.
Here is one example:

The original music, without bar-lines and using a different stem/flag system, is on top.
Two voices are singing at the same time. "Ubertagung" is the translation. Which looks simpler?
Notice all the threes in the translation! A in the original is B in the translation. In the
"Ubertagung," at letter B we see a whole note below and three half notes above. Now we know
that two half notes make a whole note, so we have to put a three on top to say "this time make it
three." Not so in the original.
I am hoping that this example alone is proof enough to the layman that triplets are not 20th
century inventions, and that splitting a whole note into three equal parts instead of two is as old
as... well, the fifteenth century.
For the more advanced readers, I have three more examples that may titillate. In the first
two examples, the original is directly above the translation. The first example is notated 6/2, and
the second measure seems to agree, but in the third and fourth measures the triplet starts on the
third beat, which is a syncopated time signature change even more sophisticated than Bernstein's 6/8 to 3/4 shifts in "America" because of the mid-stream triplet. The second example not only uses
rhythmical triplets, but carries them across the barline---and you thought Stravinsky and Ives were
the only ones to do that! The third example has the original written before the translation, off the
staff. There are two voices. In the eighth measure, the bass sings a simple 4/4 tune as the soprano
splits the same measure into ten equal parts taken as 3+3+3+1. It's notable---but is it singable?

Of course, in the fifteenth century there was no musician's union complaining about
unplayable music, for then only a few people could read music---most people were illiterate
peasants. We can assume that the composers of these pieces, who must have also been the
performers, could perform their own music and that the previous examples were performable and
performed.
Why did "musica mensurata" change to the present notation system? Encyclopedias claim
it is the complexity of mensural music that caused its downfall. In many ways this is true --- there
are quite a few special rules to be remembered. Also, a different notation system started to
emerge created by instrumentalists called "tablature." It was based on repetitious dance figures
(four beats to a measure, three beats to a measure), but it was easy to read. I will add a
hypothesis: music was handwritten, not printed. There was thus much room for isolated people
to make the same notation mean totally different things, which has made the interpretation of it
today so complicated. As the Renaissance was opening up the lines of communication, a simple
understandable notation system was proposed, and agreement was reached to drop the old system
for a more "scientific" one --- you know how smart they thought they were back then --- and
unfortunately the "complex" rhythms were dropped, too, like the baby with the bath water.
As a consequence, very old music sometimes sounds more sophisticated than the later
"developments."
Could good music be stifled by European schools of thought? No! After the
"sophisticated ones" decided to forsake their rhythms for simplicity (it was a long fight---"It took
a full century for the bar-line to be generally accepted" (International Cyclopedia of Music and
Musicians)), the "unsophisticated ones," i.e. the peasants, who never wrote anything down,
continued to sing folk songs that, it turns out, still held the old properties of "plainsong." I here
turn from the German Doctors of Musicology to an old friend: Percy Grainger.
In this report we have talked a bit about Percy's adventures with "Free Music," but, next
to his piano virtuosity, Percy was primarily known as a composer of folk song-like tunes. Like
Bartok, Percy had roamed the European countryside collecting (i.e. writing down and recording)
local folk songs and this came out in his compositions. The following example is from an actual
transcription Percy made of a song sung by a Mr. George Wray of Barton-on-Humber, England.
Mr. Wray had worked in a brickyard, as a cook and steward on ships, and finally became a coal
merchant. He could not read, write or play music---just sing. At age eight-two he sang this for
Mr. Grainger:

In 1913 a riot broke out at the premier of the rhythmically complex Rite of Spring, but in
1908 Percy Grainger was transcribing the music of common folk---music that was just as
complex.
It looks like the word "complex" is not applicable anymore. It's just music, perhaps unlike
music produced by European composers from the seventeenth to the early twentieth centuries, but
one could just as well say that it is the European music that is unlike the others.
I am now ready to explain to you my perception of rhythm. I have showed that
"complexity" has quite a long history. You have seen that a man who does not know how to read
or write music can naturally produce "complicated" rhythms without a wince. I hope you will
now accept my belief that the present musical notation system is not perfect, and can be, in fact,
quite limiting.
Back to the rope. A constant beat is knots tied at equal intervals. Notation today says,
"Multiples of two, please. Take out every other knot, or put an extra knot exactly between two
knots. Okay, you want triplets, you can have them, as long as you use all three of them so that I
can still feel that constant pulse."
I say, feel a half note pulse. It's slow, it says one thing. Now eighth notes. They're fast,
they say something else (they affect the listener in a different way). Feel a long row of triplets.
That's something else again. There are exact relationships connecting one knot to another, but
it's as if we had different ropes for the different pulses. It's not havoc---it will even be notatable --- but each speed should be at the composer's disposal for as long as he wants to use that speed,
not for as long as he is allowed to use that speed.
In music, you can't hear the next duration before it is played---you're wrapped up in time,
and that's what it's all about. We can't see when the next knot will appear----why insist that it
will appear within the notatable structure?
Instead, the composer says, "Okay, I've just had three eighth notes. Now I want this next
passage to be slower, but not half. In fact, I want the feeling created by triplets. So after the last
eighth note duration, I will flip a magical switch that makes the knots appear along a different
length of rope, at different intervals. This slower passage will have five notes to it --- then I'll flip
another switch and call up a different rhythm. I've merely changed the durations --- why do you
insist that I have six triplets when I only want five?"
In case you find the idea of placing different length rope segments in a unique order a
vague way of expressing creative composition, let me try agin. This is the "Workshop Tray
Theory of Rhythmical Composition."
Like a painter with a palette, I have a tray split into various compartments. In each
compartment is a duration --- there are eighth notes and fifth notes and a special section reserved
for useful combinations, like  and
and 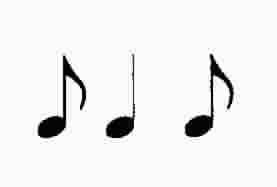 and
and  . I take durations from different trays and place
one after another. I do not lay out the durations on graph paper. When this music is played, time
will exist in an immediate sense --- you can't assume that there will be a downbeat on even-numbered seconds --- in fact, there may never be a downbeat on an even second for the rest of the
piece.
. I take durations from different trays and place
one after another. I do not lay out the durations on graph paper. When this music is played, time
will exist in an immediate sense --- you can't assume that there will be a downbeat on even-numbered seconds --- in fact, there may never be a downbeat on an even second for the rest of the
piece.
How will the trays be labeled? I am glad that once again I have found work by someone
else, a system invented by a good established composer, thus proving that I am not some crazy
kid with insufficient training asking questions that no one else cares about. Henry Cowell
composed the piece Fabric using the following notation system:

Cowell still agreed with everybody that these rhythms be contained within a measure.
Thus, the beginning of each measure of Fabric starts with a loud chord (three notes played at
once) that monotonously repeats. Interesting combinations are heard within each measure, but
the total rhythmical effect of the piece is almost boring.
Eliminate the bar-lines, let the notes mesh as they may, and perhaps then the feeling of
"fabric" will result, rather than "wallpaper".
Now we can finally notate "multiples by two." It looks like this:

There is no time signature, no meter, no bar-lines in the conventional sense. It is perfectly
readable by anyone who knows the system. It is not unplayable, but it does take a lot of practice,
and the Rhythm Combiner can help the composer of performer train his ear to the new sound of
changing speeds.
Now music like this is possible:
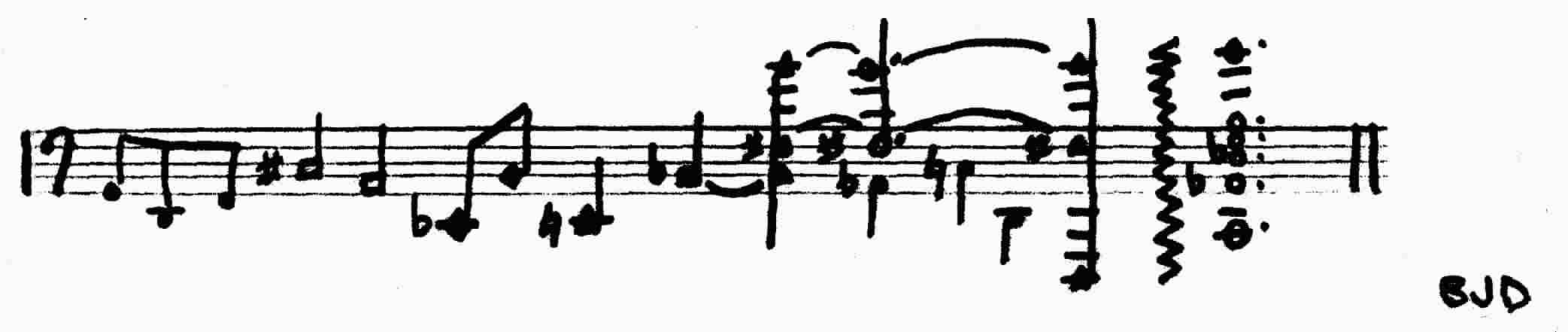
We can't expect the accent to fall where it usually does. We take each duration as it
comes. After a few hearings, we will learn some of the rhythms, and come to expect them, but
our perception of the universe has changed: what we at first thought was complex or random has
now become vital, a new way to capture time, a rhythm that makes us dance to the beat of a
different drummer.

2025 UPDATE:In June 2025, I was informed of the music of Brian Ferneyhough. According to Thomas Little, in 1981, in his piano piece Lemma-Icon-Epigram, Ferneyhough first used some fractional meters, as can be seen in this measure:

In that case, a measure of 2/10 means that the duration of the measure is a single fifth of a whole note (although it is further complicated by being subdivided into triplets). Prior to that is a measure of 4/12, a single third of a whole note (subdivided into 5 parts), and later further time signatures of x/10 and x/12, as well as a 1/20 and a 1/24. In other works by Ferneyhough, he switches freely between different tempo markings (often every measure or two) and, in interviews, he speaks about these different tempi having integral ratios to each other. As such, it is possible that, prior to 1975, Ferneyhough, seeking a way to notate his musical ideas (I had the same struggles), may have composed such a work first. For his part, Little provides a history of several composers working in what came to be labeled "The New Complexity," with similar roots to music and composers I have cited in this article, including Ives, Grainger, and Cowell. As I have written in this essay, and as Ferneyhough has said in interviews, these so-called "complexities" are merely a fault of rules applied to the notation system (other composers have extended polytonality into microtonality and even polymicrotonality (Crumb and his self-made musical instruments being the most famous example) and, a term I had not heard before, "polytempic" music). Ferneyhough is older than me by some 17 years, and, as a teacher, has many students, as well as performers willing to attempt to perform his music. He differs with the serialists, in that he sees the score as a discussion between the composer and the performer, and so is uninterested in having a computer realize a "perfect" version of the score. Although I am writing this at age 65, I am grateful to Peter Thoegerson for pointing me towards Ferneyhough although, at age 15, I was discovering what I would later call "partial triplets" independently and naturally.
Several months later, I discovered that a forgotten composer named Florent Schmitt used a fractional meter in 1906 in "La tragédie de Salomé," although the fraction was 3 and a half; subsequently, in 1909, Charles Ives used 4 and a half in his "Piano Sonata No. 1," and Edgar Varese used 3 and a half in 1921 in his "Offrandes." However, by 1916, Schmitt had used partial triplets in two measures of his Opus 64, "Ombres," as shown below:

"croches de triolet" is French for "eighth note triplets". According to musicologist Donald Byrd of Indiana University in his "Extremes of Conventional Notation" of 2018, Schmitt may be the earliest use of a "non-integer time signature numerator," although he posits that some earlier may exist. Shmitt obviously predates Ferneyhough and myself by almost sixty years. Two and two thirds over four and three and one third over four could also be written as 8/12 and 10/12, respectively.
Back to guide - Next item in guide - Back to index - Next item in index
A Musical Contrarian © 1999-2007, 2025 rights@notnicemusic.com
Last Updated: December 22, 2025
 or
or  . The slower note that lasts twice as long
is twice a quarter or a half note, which is drawn the same way as a quarter except the circle is not
filled:
. The slower note that lasts twice as long
is twice a quarter or a half note, which is drawn the same way as a quarter except the circle is not
filled:  or
or 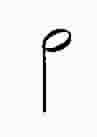 . Twice a half note is a whole note, and we drop the stem:
. Twice a half note is a whole note, and we drop the stem:  . Curiously enough, the
longer the time duration, the less there is to draw. If we were reading and singing or playing a
line of music, we would stare at the bare whole note for a long time, while we would have to
translate the filled, stemmed quarter note much faster!
. Curiously enough, the
longer the time duration, the less there is to draw. If we were reading and singing or playing a
line of music, we would stare at the bare whole note for a long time, while we would have to
translate the filled, stemmed quarter note much faster!
 or
or  . Sometimes when two or more eighth notes are next to each other we connect the
flags, e.g.
. Sometimes when two or more eighth notes are next to each other we connect the
flags, e.g.  becomes
becomes  .
.
 , etc. There is one other symbol we should
know. This does not follow our added-symbol-is shorter-duration rule. If a dot is placed after a
note, the duration is increased by half, e.g.
, etc. There is one other symbol we should
know. This does not follow our added-symbol-is shorter-duration rule. If a dot is placed after a
note, the duration is increased by half, e.g.  , a dotted quarter note, is a quarter plus eighth, or
three eighths,
, a dotted quarter note, is a quarter plus eighth, or
three eighths, 
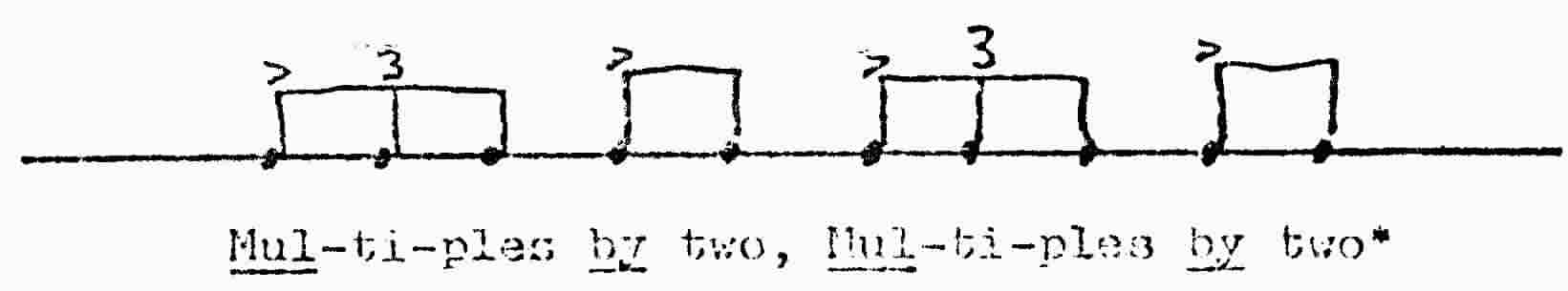


 =
=  , just as
, just as  =
=  , if we add up the number of eighth notes we get seven
per phrase. This is not that unusual---many Russian and Hungarian folk songs use this meter
(Meter is the number of units, usually quarter notes or eighths, per phrase or measure. Our
example would be written as 7/8, i.e. seven eighth note durations to a measure). What will shock
most musicians is what happens when we drop the word "and" from the phrase. It is, in fact,
unwritable. Let us look at the rope to see if we have done anything unthinkable.
, if we add up the number of eighth notes we get seven
per phrase. This is not that unusual---many Russian and Hungarian folk songs use this meter
(Meter is the number of units, usually quarter notes or eighths, per phrase or measure. Our
example would be written as 7/8, i.e. seven eighth note durations to a measure). What will shock
most musicians is what happens when we drop the word "and" from the phrase. It is, in fact,
unwritable. Let us look at the rope to see if we have done anything unthinkable.
 , which equals 3 x 2-2 x
, which equals 3 x 2-2 x 



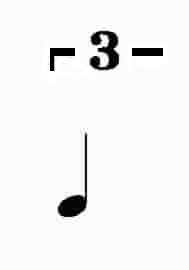 =2/3
=2/3


 and
and 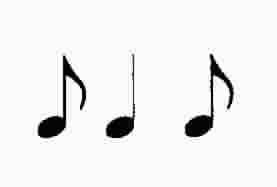 and
and  . I take durations from different trays and place
one after another. I do not lay out the durations on graph paper. When this music is played, time
will exist in an immediate sense --- you can't assume that there will be a downbeat on even-numbered seconds --- in fact, there may never be a downbeat on an even second for the rest of the
piece.
. I take durations from different trays and place
one after another. I do not lay out the durations on graph paper. When this music is played, time
will exist in an immediate sense --- you can't assume that there will be a downbeat on even-numbered seconds --- in fact, there may never be a downbeat on an even second for the rest of the
piece.